How To Think Slowly

Psychology is a weird field. I once heard a neuroscientist call it “not a science”. For much of this century, it has been haunted by the replication crisis, a big scary monster that makes scientists cry in their sleep. Freud didn’t do the field any favours either, with his unfalsifiable theories about kids having the hots for their parents.

And yet, to ignore psychology is to eat crumbs next to a feast. The mind is mysterious, but not unknowable. Psychologists have discovered many rules that predict how humans behave, even if neuroscientists can’t say yet how the brain does it. Much of our lives are made up of these predictable actions—snoozing alarms, scrolling through reels and buying stuff we don’t need when it’s on sale. Our “gut instinct” makes many of our decisions.

Apart from being hollow, slimy and often bloated, the gut is old. Its instincts were learned at a time when we lived simple lives in small groups, eating and being eaten. Why should they work in a world where lions have been replaced by recommendation engines, and fireside flirtation by Tinder swipes?

They don’t, or at least, don’t always work well. The book Thinking, Fast and Slow by late psychologist Daniel Kahneman outlines the built-in biases and blind spots of the gut. After reading it, I started to notice these biases in my daily life, like believing things just because I’ve heard them often, or not wanting to take a flight after that plane’s door fell off.

These biases can be overcome. Sometimes, just knowing they exist is enough. The availability heuristic makes us overestimate the probability of scary things like flight accidents, when they are fresh in our memory. “It’s natural to be afraid,” I can tell my gut, “but plane crashes are still exceedingly rare.”

Over time, I’ve gotten better at this “slow thinking”. I’ve learnt to recognise contexts in which the gut trips up and makes bad decisions. Here are two of them.

The Anchoring Effect

When you look for a plane ticket, the first price you see always seems outrageous. You panic. Why didn’t you buy tickets a month ago? Then you scroll down, and sigh with relief—there is a cheaper flight, though the timing sucks. This flight is only 10% cheaper than the first one you saw, and would have made you balk had it appeared at the top of the page, but now it seems reasonable.

You have been anchored.

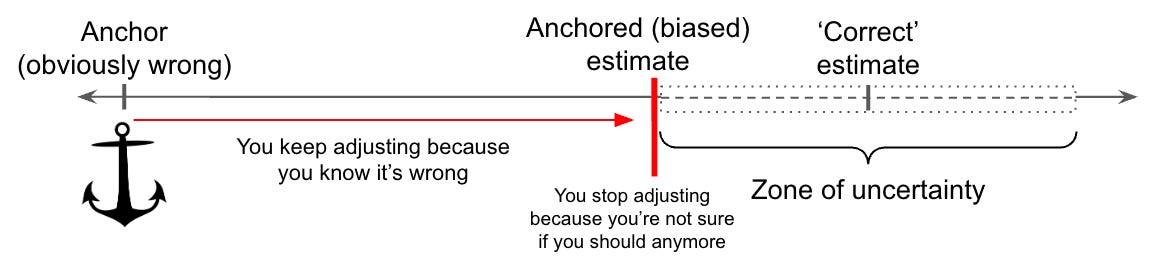
When we try to estimate a quantity, such as a reasonable price for a plane ticket, our brain starts with a number that is obviously wrong, and adjusts it up or down until it feels alright. For example, if you want to rent an apartment in Manhattan, you know you won't find anything cheaper than $1000 per month, so you think about how much more than that you can afford.

This is a clever way to solve a complex computation that depends on many things: your income and spending, saving goals, space needs, and location preferences; the New York real estate market; the type of houses your peers live in; and so on. Your brain has some idea about each of these things. Your gut synthesises this information into an emotion: $500 per month feels awesome, but $3,000 makes you anxious.

There are two issues with this system. First, the gut doesn’t move far enough away from the obviously wrong number—the ‘anchor’. Kahneman’s explanation is that we stop moving when we are at the edge of the ‘region of uncertainty’, i.e., when we are no longer sure that the number is obviously wrong. A better estimate would be the midpoint of the region of uncertainty.

The second problem is that the gut is lazy when picking an anchor. It will readily accept the number on a price tag, the salary that the hiring manager suggests, or even a random number that it knows is unrelated to the question. A chilling example of the last one is an experiment in which judges setting the length of a prison sentence were biased up or down by the outcome of a die roll.

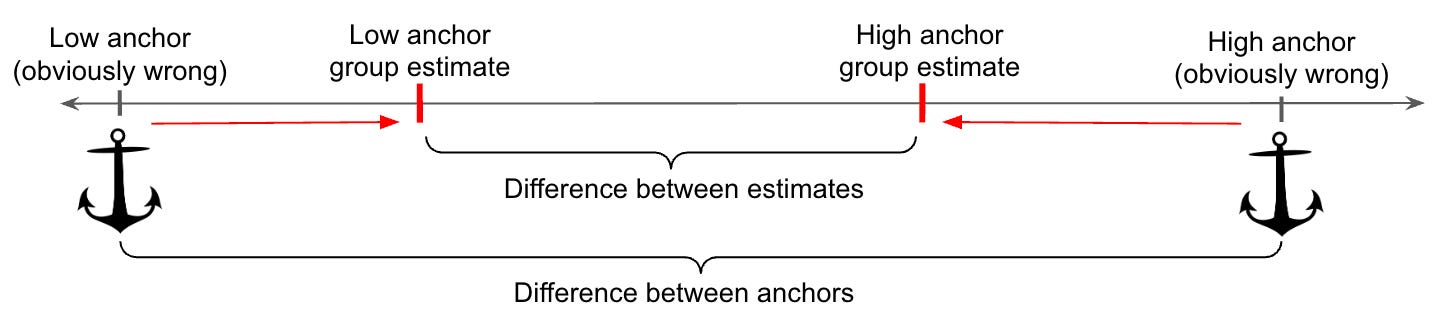
Psychologists have demonstrated the ‘anchoring effect’ in all sorts of situations. They give some people a very low anchor, and other people a very high one. The ‘anchoring index’ is the difference between the average estimates of the two groups, as a percentage of the difference between the anchors. 0% would mean there was no anchoring, and 100% would mean the groups are completely anchored.

Anchoring Index = Difference between estimates / Difference between anchors

In experiments, the anchoring index is usually between 30-50%. So as a rule of thumb, you can assume that anchors make you choose a value that is higher or lower than the ‘correct’ number by 30-50% of the distance to the anchor. For example, if the fair price of a flight ticket is $100, but the first price you see is $200, you will then estimate that $130-$150 is reasonable.

Psychological effects like anchoring apply to everyone. We think we are above this silliness; that if we had to decide how many years someone should spend in prison, we would not be influenced by the roll of a dice. But statistics don’t lie—anchoring is built into the human brain. Fortunately, many anchors are easy to avoid.

After reading Thinking, Fast and Slow, I stopped looking at price tags.

Museum gift shops are my kryptonite—full of overpriced little baubles that I yearn for. Now, I protect my purse by saying out loud what I’m willing to pay for an item, and purchase it only if it costs less than what I said. You can do something similar any time you spend money. Don’t let the marketing department tell you what a fair price is.

If you cannot avoid the anchor, Kahneman suggests two back-up strategies:

1. Assume that anchors have an effect on you. Tell yourself that you will be irrationally drawn towards the number you see.

2. Try to construct arguments against the anchor. If you had to convince someone that the price is too high, or the salary too low, or the prison sentence too long, what would you say?

Regression to the Mean

The world is more random than we think it is. The human brain is built to find patterns. “It only rains when I forget my umbrella at home,” one might think. I have been convinced for some time that the weather gods have a personal vendetta against me. Same goes for the traffic gods—they always ramp it up when I need to get somewhere on time.

Regression to the mean is a cruel illusion of pattern—an extremely counter-intuitive statistical phenomenon that makes you see causality where there is only randomness. It’s worth taking the time to fully understand it, because it might trick you into believing your friendly neighbourhood astrologer, or taking a miracle weight loss drug.

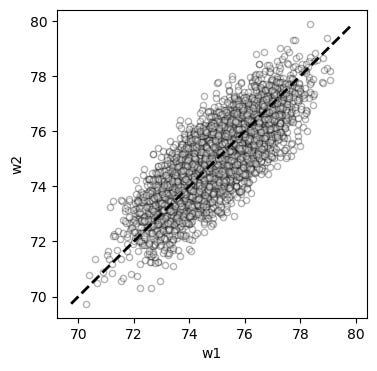
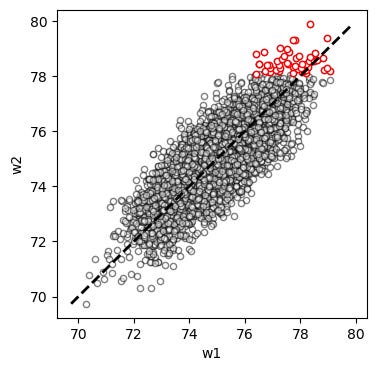
Imagine that we have measured the weight of 5000 people on a particular day, and measure it again one week later. Let’s call the two measurements w1 and w2. Since weight fluctuates, but doesn’t change a lot in one week, w1 and w2 will be similar, but not equal. If you make a graph with w1 on the X axis and w2 on the Y axis, it might look like this:

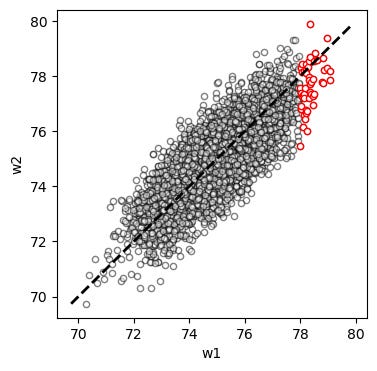
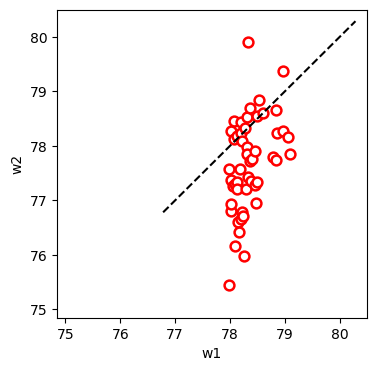
On average, w1 and w2 are almost the same (in this graph, the average difference is 0.02 kg). If they were exactly equal, they would fall on top of the dashed line (X = Y). Now imagine that we select the 50 people who weighed the most in the first measurement, and colour their dots red:

Let’s take a closer look at these people:

The values seem to be suspiciously below the X = Y line. w2 is lower than w1 for most of these 50 people. The difference between w1 and w2, the amount of weight they lost in a week, is 0.66 kg on average: 33 times the average difference of the whole group.

There’s nothing special about the values that I plotted. This pattern will show up regardless of the number of people, the mean of w1 and w2, how similar they are to each other, etc. The only requirement is that w1 and w2 are at least a little bit similar, and not exactly equal to each other. I made a thing where you can play with these numbers and generate the same graphs for yourself (will take a minute to load).

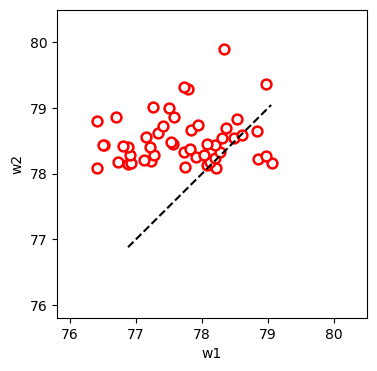
So can we conclude that the heaviest people in a group lose the most weight? Unfortunately, no. The easiest way to see that there is no ‘cause’ for this result is to look at the 50 people with the largest values of w2 instead:

These people seem to have the opposite thing going on: w1 is lower than w2 for most of them, or in other words, they seem to have gained weight (in this example, 0.81 kg on average, 40 times more than the group).

The only thing that’s happening here is regression to the mean.

When you measure something twice, if the first measurement is far from the mean, the second one is likely to be closer to the mean. When w1 is large, w2 is likely to be smaller than w1, and vice versa. If you ever need to make a quick buck selling a weight loss wonder pill, you can use this to your advantage, but don’t cite me.

Regression to the mean happens whenever two quantities are similar, but not equal, like w1 and w2. If you roll a die and get 6, the next roll will be closer to the mean if it is 2, 3, 4, or 5. The probability of this is 4/6, whereas the probability of the next roll being as far from the mean as the first one is 2/6 (if you roll a 1, or another 6).

The first roll does not have any effect on the second one; dice don’t have memory. You can, of course, roll two sixes in a row, just like a few people with high w1s had higher w2s. Regression to the mean tells you what is likely to happen, and will happen on average. If you run the experiment many times, it will show up. The following statement is also an example of regression to the mean:

Very intelligent women tend to be married to men who are less intelligent than them.

The IQs of married couples are like w1 and w2—similar, but not equal. Choose outliers among the wives, and their partners will naturally be less outlying. Of course the same thing happens with the smartest men, but it’s more fun to say it this way.

In real life, we tend to intervene when we observe extreme outcomes. Kahneman gives the example of an officer training fighter pilots. The officer reported that pilots usually flew better when he scolded them for a bad flight, but got worse if he praised them for an exceptionally good one.

A pilot’s performance on any given flight is subject to randomness. Unusually good or bad flights are likely to be followed by more average flights, thanks to regression. So pilots seem to improve when criticised, and do worse when praised. Feedback does impact human behavior of course, but regression to the mean also plays a role.

You can train your brain to recognise regression. Unlike anchoring, this is not something you can avoid, really—it’s a fact of the world—but like anchoring, if you assume it happens, you protect yourself from the pitfalls. Here are some examples:

1. Perhaps you only shout at your child when they do something atrocious. You notice that they behave better the next day. Don’t take that as an affirmation that shouting is good—it could be regression to the mean!

2. If you learn of a miracle cure for a serious disease, ask if there was a placebo group to control for regression to the mean (the sickest people in a group will appear to get better over time, just like the heaviest people appear to lose weight over time).

3. When you move to a new city, sample ten restaurants and take your guest to the best one, be prepared for disappointment—you probably caught them on an unusually good day. They might regress to the mean when you visit them again.

---

Thinking, Fast and Slow has a lot more insights where these came from.

A delightful one is the focusing illusion: nothing is as important as you think it is when you’re thinking about it. In other words, if you have to decide whether something matters to you, like buying a fancy car or running a marathon or becoming paralysed from the neck down, you will likely overestimate its impact on your life. Most people dwell much less than they thought they would, on the car or marathon or full-body paralysis, after it happens.

Then there is the peak-end rule: the best or worst part of an experience, and its last moments, disproportionately affect your opinion of it. You don’t consider the entirety of an experience when judging how good or bad it was. This even applies to your whole life! Consider this question: Is a wonderful, extraordinarily amazing life improved or made worse by adding five average years to it?

If you enjoyed this, pick up the book and let me know your thoughts.